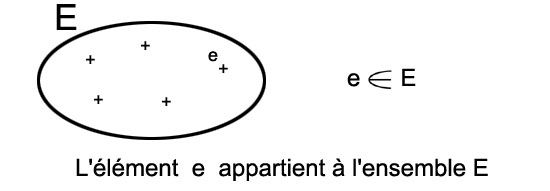
Les ensemblesUne branche des mathématiques, la théorie des ensembles, permet de traiter de manière formelle les collections et les classes d'objets. Nous devons cette théorie au mathématicien Cantor (1845-1918), qui en a profité pour donner à la notion d'infini une rigueur mathématique. Cantor et ses continuateurs ont réussi à reconstruire l'ensemble des mathématiques à partir de la théorie des ensembles. C'est une construction belle et ambitieuse, évidemment très complexe. Mais elle part de notions simples et relativement concrètes, qui peuvent nous aider dans la vie de tous les jours. Un motif suffisant pour les présenter brièvement ci-dessous. Une collection d'objetsUn ensemble est une collection d'objets, que l'on appelle éléments: on dit que les éléments appartiennent à cet ensemble. Cela se représente classiquement par le dessin et la notation que voici
Il y a deux façons de définir un ensemble: - soit en donnant la liste de ses éléments (on
dit alors qu'on le définit "en extension"); Egalité, inclusion, partitionOn dit que deux ensembles sont égaux
lorsqu'ils contiennent exactement les mêmes éléments.
Lorsqu'un ensemble ne contient aucun élément, on dit
que cet ensemble est l'ensemble vide,
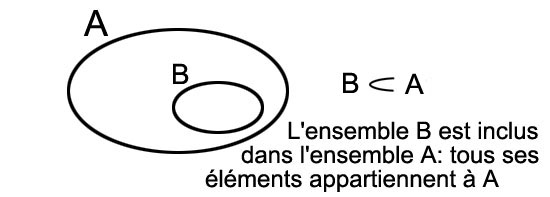
et son symbole est Lorsque tous les éléments d'un ensemble B appartiennent à l'ensemble A, on dit que A est inclus dans B, ce qui se représente
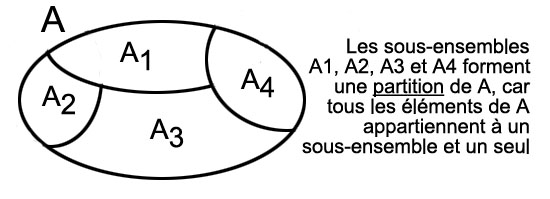
On dit aussi que B est un sous-ensemble de A. Lorsque plusieurs sous-ensembles de A sont tels qu'aucun n'est vide et que tous les éléments de A appartiennent à un de ces sous-ensembles et à un seul, on dit que ces sous-ensembles forment une partition de A.
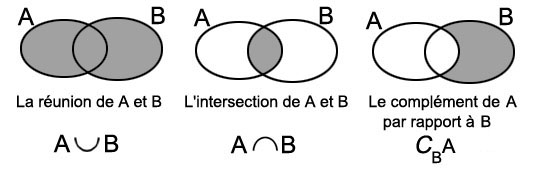
Opérations sur deux ensemblesRetenons les trois opérations les plus connues (la portion en grisé montre chaque fois le résultat).
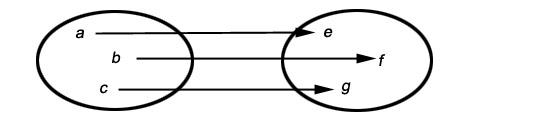
RelationsOn peut définir des relations entre les éléments de deux ensembles. Cela introduit à la notion de fonction.
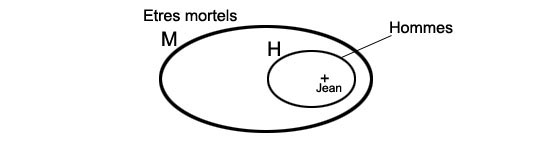
CardinauxLe cardinal (souvent représenté par le symbole #) d'un ensemble correspond au nombre de ses éléments, ce qui introduit à tout le calcul numérique. Le langage des ensemblesLe syllogisme suivant est très connu.
Voici comment exprimer cela en termes d'ensembles.
A partir de cet exemple très simple, on peut deviner comment représenter des raisonnements plus compliqués. Les ensembles dans l'enseignementAu cours des années 1960 et 1970, plusieurs mathématiciens enthousiastes et pédagogues ont voulu construire un enseignement des mathématiques cohérent basé, depuis la maternelle jusqu'à l'université, sur la théorie des ensembles. Malgré de belles réussites, cette vision ne s'est pas imposée, et l'enseignement général d'aujourd'hui ne reprend que des bribes de la théorie des ensembles. |