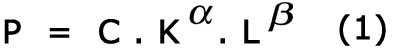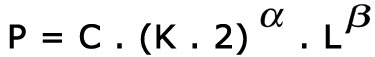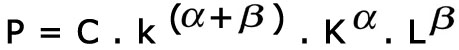Fonction de production

Les économistes n'ont pas manqué de chercher à exprimer mathématiquement la quantité de produit en fonction de celles des facteurs de production.

Quelle forme doit avoir une telle fonction? Essayons de la construire intuitivement.

Partons du cas où n'existent que deux facteurs de production. Par exemple, lorsque l'on se contente de distinguer le capital (K, pour Kapital) et le travail (L, pour Labour).

Sans doute le produit d'une multiplication

Lorsqu'un des deux facteurs se réduit et même s'annule, la production, elle aussi, se réduit puis s'annule. Cela nous pousse à écrire (cela ressemble à un jeu de mots) que la quantité de produit P est égale à un produit, où interviennent chacun des deux facteurs:

P = ... x K x ... x L x ...

Mais avec des freins

Cependant, l'expérience montre que

Dans la formule, il faut donc appliquer des freins à K et à L pour diminuer leur impact sur le produit. Cela peut se faire par l'application, à K et à L, d'exposants inférieurs à un. Appelons-les et . La fonction devient alors

(où C est une constante appropriée)

On voit bien que, si l'on multiplie K par 2, la production devient

La production n'est dès lors multipliée que par 2 exposant alpha, soit par moins que deux. C'est une manière de réexprimer la loi des rendements décroissants.

Elasticité

Les exposants et déterminent donc la sensibilité de réaction de la production à une modification des facteurs de production K et L. C'est ce que les économistes appellent l'élasticité: le raport entre la variation d'un phénomène résultant et celle du phénomène qui le cause.

Rendements d'échelle

Dans la formule (1) ci-dessus

si l'on multiplie K et L par un même coefficient k, P devient

On parle ici de rendements d'échelle :

si est supérieur à 1, ils sont croissants (économies d'échelle)
si est inférieur à 1, ils sont décroissants
si est égal à 1, ils sont constants

Cobb-Douglas

	La fonction numérotée (1) ci-avant a été mise en lumière et testée en 1928 par l'économiste Paul Douglas et le mathématicien Richard Cobb. Ils ont montré qu'elle convenait bien à la description de l'évolution de l'économie américaine entre 1899 et 1920.
	Paul Douglas

Depuis, cette fonction s'est montrée particulièrement utile aux économistes, aussi bien pour l'étude de l'économie globale (macroéconomie) que pour celle d'industries particulières, le plus souvent avec l'hypothèse que = 1 (rendements d'échelle constants).

La fonction peut d'ailleurs être généralisée à un nombre quelconque de facteurs de production, chacun étant affecté de son élasticité propre. Voir par exemple l'énoncé succinct qu'en donne Wikipedia ICI.

Il faut cependant noter deux points importants.

Le premier, c'est que la fonction de Cobb-Douglas ne s'appuie sur aucune étude des processus techniques et organisationnels de la production.

Le second point est que, sur un plan strictement mathématique, l'addition de deux productions décrites par les mêmes élasticités et ne donne pas une production aux élasticités et , SAUF dans le cas particulier où L1/L2 = K1/K2.

Ces points sont notamment discutés ICI, ce texte anglais comportant un développement mathématique simple, bien relié aux réalités économiques.