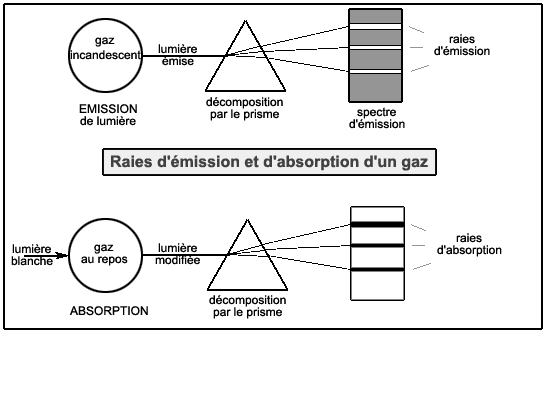
Le modèle de Bohr

Spectres et raies

Cette fois, c'est l'étude des raies spectrales qui allait permettre de dépasser le modèle planétaire de Rutherford.

Que sont les raies spectrales?

On sait depuis Newton qu'en faisant passer une lumière blanche dans un prisme, on la décompose en une infinité de couleurs, couvrant un large spectre de longueurs d'onde. Que se passe-t-il si l'on décompose de la même manière une lumière émise par un gaz (l'hydrogène, par exemple) porté à l'incandescence?

Il se passe quelque chose d'étrange: au lieu d'un spectre continu, on obtient un spectre réduit à quelques fines zones, ou raies. Ces raies sont en quelque sorte la signature du gaz, qui le distingue des autres au point qu'elles permettent de l'identifier lors de l'analyse de la lumière émise par les étoiles les plus lointaines. On parle de raies d'émissions.

Un phénomène similaire se manifeste lorsque le gaz est au repos, et qu'on le fait traverser par un rayon de lumière blanche: si on analyse ce rayon après la traversée du gaz, on constate des lacunes (raies noires) dans son spectre. Et ces raies sont situées au même endroit du spectre que les raies d'émission!

Pourquoi cette émission et cette absorption dans quelques longueurs d'onde seulement? Faute de comprendre cette discontinuité, le physicien suisse Balmer, peu après 1890, parvint à établir une formule permettant de calculer les longueurs d'onde de ces raies, du moins pour l'hydrogène. Voici sa formule, qui donne la longueur d'onde L_n de la nème raie du spectre de l'hydrogène:

1/L_n = R ( (1/2²) - (1/n²) )

où R est la constante de Rydberg, propre à chaque élément.

R_H = constante de Rydberg pour l'hydrogène
R_H = 109 700 par cm

Dans cette formule, chaque raie (dans le domaine du visible) correspond à une valeur entière de n: 3, 4, 5,...

Etonnant: cette formule fait donc correspondre chaque raie visible de l'hydrogène à un nombre entier 3, 4, 5, ... !

Bientôt, d'autres raies de l'hydrogène furent découvertes, notamment dans l'infrarouge et l'ultraviolet, ce qui permit de généraliser la formule de Balmer

1/L_n = R_H ( (1/m²) - (1/n²) )

où m remplace la valeur 2 de la formule précédente par différentes valeurs entières (m = 1, 2, 3, ...), tandis que les valeurs (entières) de n doivent y être supérieures à m.

La lumière par grains

Il y avait un point commun entre la discontinuité mise en formule par Balmer et les idées de Planck (1900), bientôt reprises par Einstein (1905), selon lesquelles la lumière était émise par bouffées, chaque bouffée ayant, pour une longueur d'onde , une énergie h x , où h est appelé constante de Planck et a la valeur

h = 6,62.10^-34 Joules x secondes

Il appartint à Bohr d'élaborer, en 1913, un nouveau modèle de l'atome qui tenait compte de tout ce qui vient d'être dit.

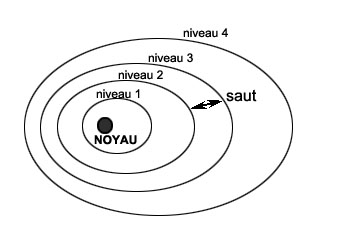
Par exemple, le spectre de l'hydrogène contient une raie de longueur d'onde 656,3 nanomètres. Cette raie correspond au saut d'un électron du niveau 2 vers le niveau 3 (raie d'émission) ou vice-versa (absorption).

Très schématiquement (rappelons que les échelles ne sont ici pas respectées):

Un noyau central composé de protons et de neutrons; des électrons tournant autour de lui sur des orbites soigneusement étagées: telle est l'image de l'atome qui s'imposa à partir de 1913.

Application:

Dans la couche 3 (n = 3) de tout atome, il y a ainsi trois sous-couches, numérotées
l = 0,1,2.
Dans la première de ces sous-couches (l = 0), les électrons ne peuvent avoir que le nombre quantique magnétique m = 0. On peut donc y trouver deux électrons, de spins s = -1/2 et +1/2.
Dans la seconde sous-couche (l = 1), les électrons peuvent avoir des nombres magnétiques de -1, 0 ou 1 et des spins de -1/2 ou +1/2. La sous-couche peut donc contenir 6 électrons.
Dans la troisième sous-couche (l = 2), les électrons peuvent avoir des nombres magnétiques de -2,-1,0,1 ou 2 et des spins de -1/2 ou +1/2. La sous-couche peut donc contenir 10 électrons.
Au total, la couche 3 peut donc contenir 2+6+10 = 18 électrons.