Relation linéaireDeux grandeurs, avons-nous vu, sont proportionnelles lorsqu'elles sont liées par une relation telle que A = k.B Ceci peut s'exprimer dans le langage des fonctions. On utilise alors le plus souvent les lettres y et x plutôt que A et B, tandis que la lettre a tient lieu de coefficient de proportionnalité: y = a.x Si l'on fait varier librement x, la valeur de y sera toujours a.x. Cela se représente graphiquement comme suit.
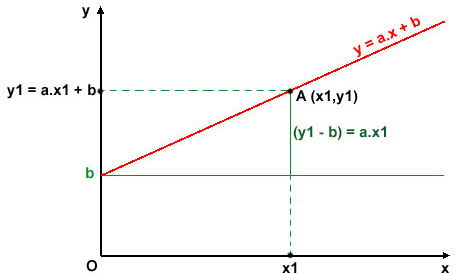
C'est une droite, ce qui a conduit à appeler cette fonction fonction linéaire. On retrouve d'ailleurs l'image des piquets alignés, que nous avons utilisée pour introduire la proportionnalité. Cependant, cette ligne droite a la particularité de passer par le point d'origine des deux axes du graphique. Autrement dit: si x = 0, alors y = 0. Une fonction linéaire (représentée par une droite) peut passer à côté de l'origine O. Dans ce cas, si x = 0, alors y n'est pas nul; il est, par exemple, égal à b. Et au lieu que y soit proportionnel à x, ce sera (y - b) qui le sera: (y - b) = a.x ou encore y = a.x + b, forme la plus générale sous laquelle
s'écrit l'équation
d'une fonction linéaire. Voici la représentation graphique
correspondante, où le point A est le point de coordonnées
SimplicitéLa fonction linéaire se distingue par sa simplicité, par opposition aux fonctions où l'une ou l'autre des variables intervient avec un exposant, ou au dénominateur, ou comme exposant... Cette simplicité facilite les calculs et les représentations graphiques. C'est pourquoi les utilisateurs de mathématiques, tels les physiciens, les économistes, les ingénieurs, etc. s'efforcent toujours d'exprimer les lois et phénomèns au moyen de fonctions linéaires (ce qui est loin d'être toujours possible!). |