Sinus, cosinus, etc.

Partir de l'angle?

Nous avons vu qu'il est possible de calculer la hauteur d'un piquet situé à une certaine distance si l'on connaît distance et hauteur d'un autre piquet, aligné sur le premier par rapport à l'observateur. Par exemple:

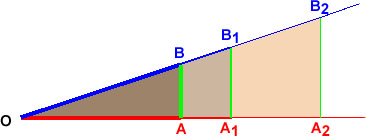
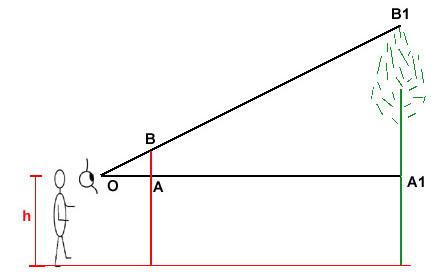
A2B2 = AB x OA2/OA

C'est aussi très commode pour évaluer à distance la hauteur d'un grand arbre. Attention cependant à tenir compte de la taille h de l'observateur!

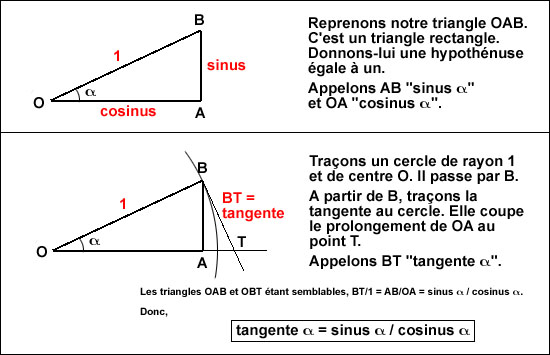
A1B1 = AB x OA1/OA

donc hauteur de l'arbre = h + A1B1 = h + (AB x OA1/OA)

Toutefois, cette méthode oblige à planter un piquet et à mesurer trois longueurs: AB, OA et OA1 (sans compter h). Ne pourrait-on exploiter la mesure de l'angle de vision pour calculer plus simplement?

Effectivement, pour le même angle , tous les triangles (rectangles) OAB, OA1B1, OA2B2 sont semblables, et leurs côtés sont proportionnels:

AB/OA = A1B1/OA1 = A2B2/OA2

Appelons T() cette proportion. Il nous suffit de la connaîre pour pouvoir calculer AB, A1B1 et A2B2 à partir de OA, OA1 et OA2. Par exemple:

A2B2 = OA2 x T( )

Sinus, cosinus, tangente

Prenons les choses un peu plus systématiquement, et appelons-les par leurs noms officiels: sinus, cosinus, tangente (en abrégé sin, cos et tg)

Si nous disposons d'une table (ou d'une machine à calculer) qui nous donne, pour chaque valeur de l'angle , la valeur de ses sinus, cosinus et tangente, il nous est facile de calculer la hauteur de notre arbre par la formule AB = OA x tg

Sur cette base très simple, s'est bâtie toute la trigonométrie, avec son impressionnant cortège de formules, utilisées par exemple en topographie et en astronomie, mais aussi dans toutes les disciplines faisant appel à des fonctions périodiques, par exemple en électricité.

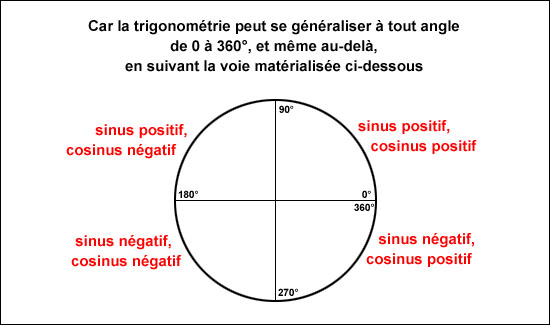
En suivant la valeur du sinus entre 0 et 360°, on comprend pourquoi sinus est une fonctiion périodique de :