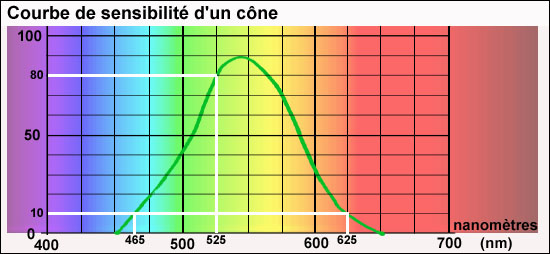
L'oeil et les mélanges de couleursEn physique, pas de mélanges de couleurs!On pourrait imaginer que deux rayons de couleurs (de longueurs d'onde) différentes se combinent pour former un rayon d'une troisième. Une troisième dont la longueur d'onde serait par exemple la moyenne des deux premières, ou leur moyenne pondérée par l'intensité des rayons... Non! Dans le monde de la physique, les couleurs ne se mélangent pas. Le mélange s'effectue lors de leur perception par un être vivant. Formule lapidaire: c'est dans notre oeil et notre cerveau que s'effectue le mélange des couleurs! Mais comment, ce mélange? Des cônes: dites-moi "longueur d'onde", je réponds "intensité"La rétine de l'oeil est tapissée de récepteurs, de capteurs spécialisés appelés cônes. C'est par eux que s'opère la perception des couleurs. Y a-t-il un type de cône pour chaque longueur d'onde? Non, il en faudrait beaucoup trop, une infinité même. Alors, y a-t-il un seul type de cône, laissant le cerveau se débrouiller avec des messages du genre "moi, capteur, ai reçu une lumière de longueur d'onde 500 avec une intensité 2 et une lumière de longueur d'onde 650 avec une intensité 4 et ... etc."? Pas davantage. Un cône est sensible à toute une gamme de longueurs d'onde, mais cette sensibilité dépend de la longueur d'onde. Et cela se traduit par une courbe de sensibilité.
Lorsqu'il reçoit un rayon de
Objection: comment, avec ce système, le
cerveau pourrait-il comprendre de quelle couleur il s'agit? Avec
cette courbe en cloche, "intensité 10" pourrait
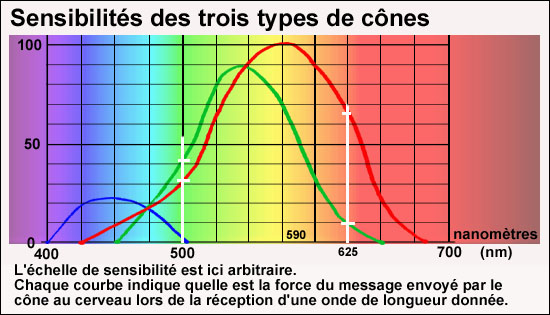
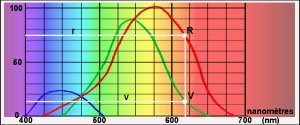
tout aussi bien se rapporter à Réponse: l'objection serait valable s'il n'existait qu'une sorte de cône. Mais il en existe trois sortes. L'une, plus sensible au rouge, la deuxième plus sensible au vert, la troisième plus sensible au bleu. Et chaque type de cône a sa courbe de sensibilité. Les messages des trois types arrivent séparément au cerveau.
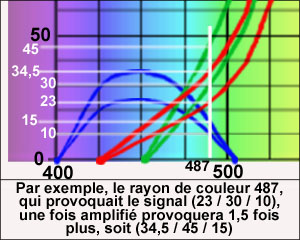
Par exemple, pour un rayon de
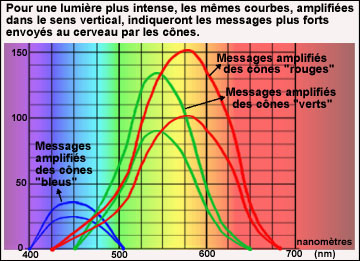
De même, pour Amplification
Comment dès lors se mélangent les couleurs?C'est sur la base de ce qui précède (est-ce simple? est-ce compliqué?) que le cerveau discernera pour nous la magnifique palette des couleurs visibles. A noter que la physiologie de l'oeil nous apprend que l'opération ci-dessus s'effectue séparément pour chaque zone de la rétine, de sorte que ce sont des millions de messages qui parviennent au cerveau à chaque instant. Combinaisons de couleurs pures
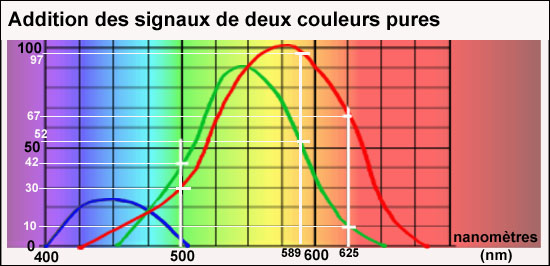
Voyons comment se combinent sur notre rétine deux couleurs pures de longueurs d'onde 625 (à dominante rouge) et 500 (à dominante verte). Voici les réponses des cônes "rouge" et "vert" (nous négligeons les cônes "bleu", très peu concernés).
Oui, les excitations des cônes, provoquées par les
deux couleurs, s'additionnent, et c'est la somme qui est envoyée
au cerveau: (97 - 52 - 0). Ce message, le cerveau peut l'interpréter
en termes de couleur: comme on le voit sur l'image, c'est le même
message qu'il recevrait si on avait éclairé la rétine
par la couleur de C'est un hasard, car la combinaison de deux couleurs pures ne conduit pas toujours à une autre couleur pure.
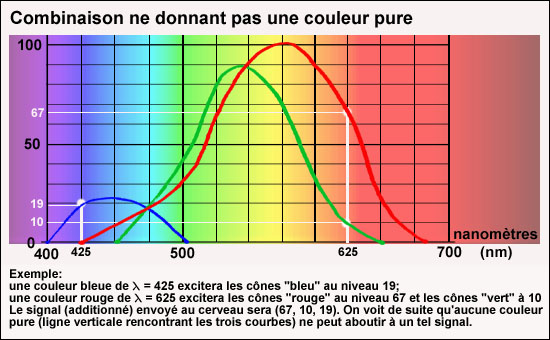
Est-ce à dire que, en l'absence de cet alignement vertical, aucune couleur ne sera perçue? Pas du tout. Aucune couleur pure (de l'arc-en-ciel) ne sera perçue, mais le cerveau construira, à partir du signal reçu, une couleur qui nous paraîtra plus ou moins voisine de certaines couleurs pures, car correspondant à un signal plus ou moins proche des leurs. Voisines, oui. Mais pas toutes!L'impression de voisinage joue donc un grand rôle dans la manière dont nous concevons le monde des couleurs. Et "voisinage" doit se comprendre au sens physiologique: proximité des niveaux des signaux envoyés au cerveau, respectivement par les cônes "rouge", "vert", et "bleu". (50 - 35 -10) est proche de (55 - 32 - 12) Il nous suffit de regarder à nouveau les trois courbes de sensibilité pour deviner que certaines combinaisons de couleurs pures ne sont voisines d'aucune autre couleur pure: c'est surtout le cas des combinaisons (bleu + rouge).
C'est pourquoi nous percevons des couleurs qui sont totalement étrangères au spectre solaire (arc-en-ciel): ce sont les couleurs appartenant au continuum rouge vers bleu. Voici une manière de voir ce continuum.
Dans le voisinage de ce continuum se trouvent trois couleurs très connues:
le magenta: beaucoup de rouge, beaucoup de bleu Les combinaisons en pratiqueMélanger des couleurs de manière à ce que
les signaux perçus s'additionnent se pratique par exemple Et la palette du peintre? Là, il n'est pas question d'addition. Nous en parlons par ailleurs. |
||||||||||||||||||||||||