Les catégories de nombresLes nombres ont sans doute été d'abord inventés pour compter. A strictement parler, il suffit pour cela de nombres dits "naturels" (1, 2, 3, ...), encore que très vite le besoin de notions telles que un demi, ou un quart (le demi du demi) puisse se révéler. Au fur et à mesure du développement des sociétés (commerce, agriculture, ...) et de la science (géométrie, astronomie, ...), et lorsqu'il ne s'est plus agi seulement de compter, mais aussi de mesurer, d'autres catégories de nombres sont apparues. Il n'est pas mauvais de les présenter rapidement, tout en faisant remarquer que ce vocabulaire est surtout utile aux mathématiciens. Les nombres naturels (N)Les nombres naturels sont ceux que l'on rencontre dans l'activité naturelle de dénombrement. Les mathématiciens appellent N (zéro inclus), ou N* (zéro exclu) l'ensemble de ces nombres. Les nombres entiers (Z)Voici, pour cette année, l'évolution de mon troupeau
de moutons: Et l'on appelle Z ("nombres entiers") l'ensemble formé des nombres naturels, des nombres relatifs et du zéro. Les nombres décimauxLes nombres décimaux (c'est un terme réservé au système décimal) sont ceux qui ne sont pas entiers. Ils s'écrivent avec une virgule, et les chiffres qui apparaissent derrière cette virgule indiquent que l'on ajoute au nombre une certaine quantité de dixièmes, de centièmes, de millièmes, etc. Autrement dit, la structure du nombre a été généralisée
aux puissances négatives de 10. Ainsi, le nombre 723,68 est
égal à Les nombres rationnels (ou fractionnaires) (Q)Les nombres rationnels sont ceux qui peuvent s'écrire comme le résultat de la division d'un nombre entier par un nombre entier (autrement dit: une fraction). Les mathématiciens appellent Q l'ensemble des nombres rationnels. Tous ces nombres ont
Les nombres irrationnels (non fractionnaires)Les nombres irrationnels sont ceux qui ne sont ni entiers ni rationnels. Ils ont un nombre infini de décimales, se suivant sans aucune périodicité. Ils ne peuvent s'obtenir par division de nombres entiers. On y trouve entre autres les racines carrées des nombres qui ne sont pas des carrés parfaits, ainsi que les autres racines non entières . Exemple 1: Les nombres réels (R)Les nombres réels regroupent les rationnels et les irrationnels, c'est l'ensemble de tous les nombres que l'on utilise généralement. Deux sous-ensembles particuliers
Le nombre irrationnel
|
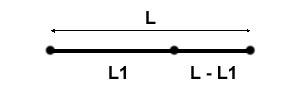
Calcul du nombre d'or Considérons L/L1 comme étant
la valeur x à chercher. |
| Le nombre d'or est 1,61803398... |
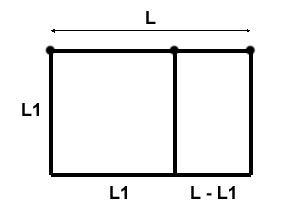
Cette proportion nous permet de dessiner, à partir du segment précédent, deux rectangles réputés particulièrement bien proportionnés, car ayant le nombe d'or comme rapport entre leurs côtés:
 |
(sans
garantir qu'ici la gestion de votre écran permet la
reproduction exacte de la proportion voulue) |
Sans nier les belles proportions de ces rectangles,
certains
constatent
- qu'aucune enquête n'a pu démontrer le succès
indiscutable de cette proportion,
- que peu de grandes oeuvres l'ont utilisée,
- et que celles où elle est employée n'en ont pas
tiré une réputation particulière.
D'autres, au contraire, multiplient les démonstrations (notamment pour les objets naturels), si bien que le nombre d'or reste une source de controverses.