Mesures trompeusesQue pensez-vous des deux opérations suivantes: Ces mesurages vous paraîtraient sans doute étranges. Et pourtant, nous procédons de la sorte dans certains cas. La monnaie: un étalon instableBien loin d'être conservé, comme le mètre de platine, dans un pavillon protégé, l'étalon monétaire est soumis à la loi de l'offre et de la demande: lorsqu'une monnaie est très demandée dans le monde, sa valeur augmente par rapport aux autres monnaies. Par ailleurs, lorsqu'un pays émet trop de monnaie par rapport au volume des biens disponibles, la valeur de sa monnaie diminue, il y a inflation, les prix des biens augmentent. La monnaie est un étalon variable. En 1944, à Bretton Woods, un accord international visant à plus de stabilité en période de reconstruction a mis en avant l'étalon-or. Le dollar, principale monnaie mondiale, lui était lié par le rapport de 35 dollars l'once d'or, et les autres monnaies mondiales étaient liées au dollar par des parités fixes. Ce système a prévalu de 1946 à 1971. En 1971, les Etats-Unis ont détaché le dollar de l'or. En principe, les cours des monnaies sont devenus flottants. Mais les pays peuvent, par des décisions individuelles ou collectives, fixer le cours de leur monnaie par rapport à une autre monnaie dite "de référence". Cela suppose que si leur monnaie est peu demandée ils devront en acheter eux-mêmes en vendant de l'or ou d'autres monnaies qu'ils détiennent. Ceci n'est possible que dans une certaine mesure: si un pays n'y parvient plus, il devra dévaluer sa monnaie. Aujourd'hui, les grandes monnaies mondiales (dollar, euro, yen, livre) sont "flottantes": leurs cours varient en permanence en fonction de l'offre et de la demande, ... et il en est de même du cours de l'or, le plus sopuvent exprimé en dollars. Depuis la création de l'euro, le rapport entre l'euro et le dollar a varié quasiment du simple au double: entre 0,8 et 1,5, ce qui est loin d'être anodin et a beaucoup de conséquences pour le commerce international. Mesurer l'immatériel? Le cas de l'intelligenceUne des valeurs immatérielles les plus étudiées est l'intelligence. Il va de soi qu'on ne peut mesurer une quantité d'intelligence au moyen d'un étalon-unité. On procède alors d'une manière qui n'est pas sans susciter des malentendus. On met sur pied un test d'intelligence, c'est-à-dire une batterie de questions qui rapportent chacune au sujet testé un certain nombre de points, que l'on additionne ensuite pour obtenir un résultat global, que l'on appelle "quotient intellectuel" (QI). Tout ce que l'on peut faire au moyen d'un tel test, c'est classer les sujets dans l'ordre de leurs résultats. Il n'est pas question, par exemple, de déclarer "tel sujet, qui a obtenu 140, est deux fois plus intelligent que tel autre ayant obtenu 70". Pour accroître la pertinence de ce classement ordinal, et pour permettre de meilleures comparaisons entre différents tests, les spécialistes procèdent à deux opérations conjointes. 1. L'étalonnage du testL'étalonnage consiste à soumettre à ce test
un échantillon représentatif d'une population de référence
(p.ex. celle d'un pays, d'une classe d'âge, ...). 2. La normalisation du testLa normalisation du test consiste à faire en sorte que les
résultats obtenus par la population de référence
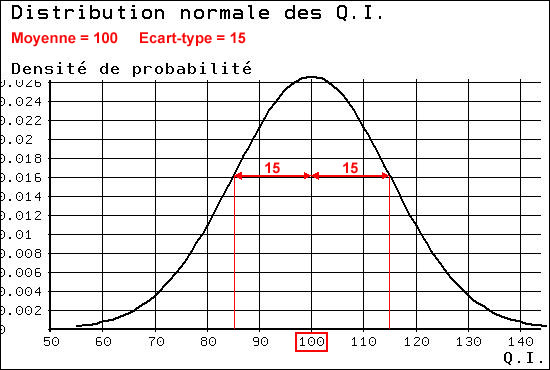
répondent à une distribution "normale",
caractérisée par une moyenne et un écart-type
( Cette normalisation exige de fines manipulations (voir par ex.
ICI),
consistant notamment à La normalisation d'un test présente un double avantage:
|