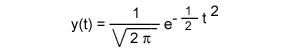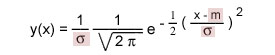Loi normale en continuDu discret au continuAu chapitre précédent, nous avons fait la connaissance de la loi de probabilité dite "normale", et de la forme particulière de sa courbe (dite "en cloche"). Cet exposé n'était valable que dans les cas où l'on est limité à des nombres entiers, comme dans les tirages au sort. Si l'on doit traiter des valeurs décimales, on ne peut plus travailler avec des formules telles que Nx(N-1)x(N-2) ni N! (factorielle de N), ni donc avec les formules des arrangements ou des permutations (qui sont, dit-on, de la mathématique "discrète").
Pour traiter en probabilité, par exemple, les tailles des individus, il faut une autre mathématique: la mathématique du continu. Eh bien, la loi "normale" existe aussi dans le continu, et nous allons retrouver la courbe en cloche, arrondie cette fois, non plus en escaliers. Mais pour ce faire, il faudra aborder les choses sous un angle un peu différent. La loi normale en continuIl faudra d'abord parler de variable aléatoire: c'est une variable pouvant prendre au hasard diverses valeurs. Par exemple: la taille des êtres humains. Supposons que nous connaissions, au millimètre près, les tailles de 10 000 êtres humains. Choisissons un de ceux-ci au hasard. Poser la question "quelle est la probabilité que cet homme mesure exactement 1 m 75?" n'a pas beaucoup de sens. Dans la mathématique en continu, il faudra plutôt se demander, par exemple: "quelle est la probabilité qu'il mesure entre 1 m 745 et 1 m 755". Naturellement, plus l'intervalle choisi autour de 1 m 75 est grand, plus grande sera la probabilité. Aussi, pour examiner l'évolution de la probabilité en fonction de la taille, il faudra tenir compte de cet intervalle. Plus précisément, nous mettrons ce dernier au dénominateur et nous nous intéresserons à la valeur suivante:
Une courbe de baseAprès de longs travaux à rebondissements (voir p. ex. l'exposé pédagogique de Bernard BRU), les mathématiciens ont conclu que, dans les cas de phénomènes dépendant d'un ou de plusieurs facteurs relevant du seul hasard, la valeur de cette fraction évoluait selon la formule
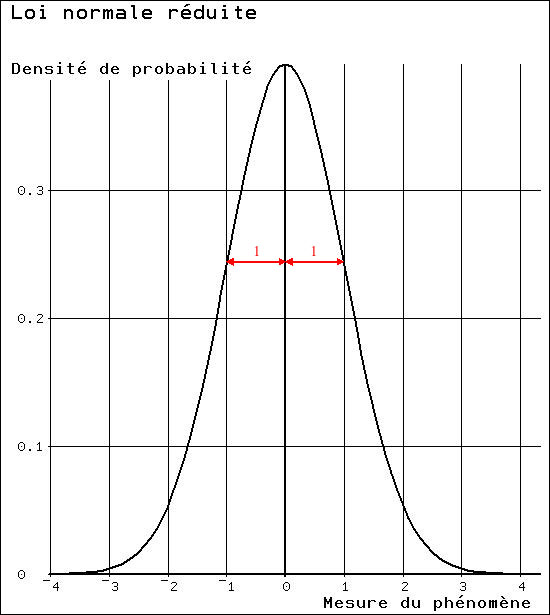
dite "loi normale réduite". C'est une loi de distribution, qui donne, en fonction de la taille t, non pas la probabilité, mais la densité de probabilité attachée à cette taille. En voici la courbe.
On est immédiatemnt frappé par sa ressemblance avec la courbe de distribution des tirages à pile ou face. Nous tenons donc là une courbe très utile pour l'examen de phénomènes dépendant du hasard. Pourquoi "réduite"?Loi normale réduite, premièrement, parce que la moyenne des mesures observées est de zéro. Deuxièmement, parce que la dispersion des mesures est ramenée à un cas particulier. Cette dispersion est en quelque sorte la largeur de la courbe, habituellement mesurée comme la moitié de la distance qui sépare les deux "points d'inflexion" de la courbe.
Dans le cas de la courbe normale "réduite", l'écart-type est égal à un. On peut facilement transformer la formule ci-dessus pour l'adapter
à des cas où Pour cela, dans la formule précédente, nous exprimons - la densité de probabilité en multiples de D'où la nouvelle formule de la densité de probabilité:
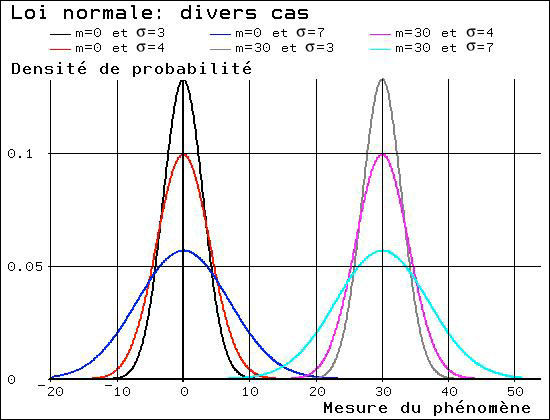
qui permet de faire varier la courbe en jouant
sur les valeurs de m et
Cette fonction et sa courbe se prêtent alors à une utilisation pratique. |