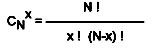Binomiale, PoissonIl existe d'autres lois de probabilité que la loi normale. Loi binomialeLa loi binomiale, elle aussi consacrée au cas de nombres discrets, est en quelque sorte une extension de la loi normale. En effet, la loi normale s'intéresse aux séries de tirages à pile ou face (de probabilité 1/2). La loi binomiale s'intéresse aux séries de tirages de probabilité quelconque. Si on effectue N tirages pour lesquels la probabilité de réussite est p (par exemple, aux dés, la probabilité d'obtenir le 4 est de 1/6), la probabilité d'obtenir x fois cette réussite est donnée par la formule
où CNx est le nombre de combinaisons sans répétition de N objets x à x, donné par la formule
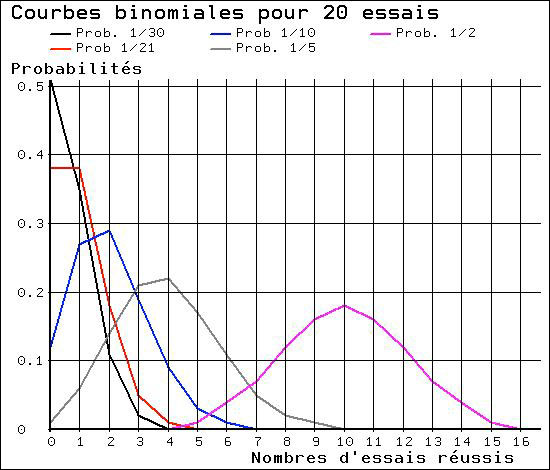
Cette loi de probabilité est appelée loi binomiale. Voici quelques cas de courbes qui la représentent, pour 20 essais.
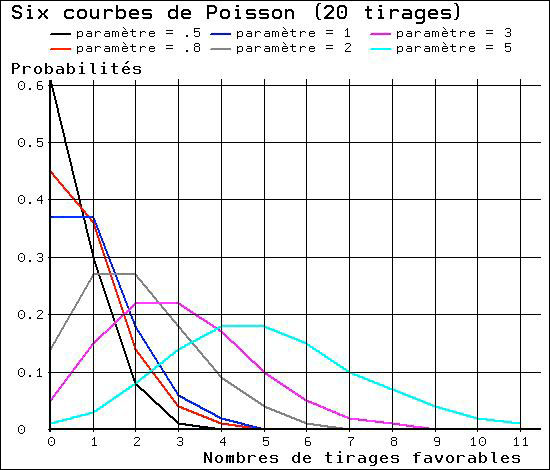
Loi de PoissonEn examinant les courbes ci-dessus, on remarquera aussi que plus la probabilité de tirage est petite, plus la courbe est asymétrique. Ces courbes asymétriques peuvent être exprimées mathématiquement par la formule de la loi de Poisson
où le paramètre Voici six courbes de Poisson, correspondant aux
coefficients
Comme on l'a déjà vu plus haut, cette loi convient bien pour les événements de faible probabilité. On trouvera ICI
une application de la loi de Poisson aux accidents de travail. Une
bonne approximation de la distribution y a été trouvée
à partir de la seule moyenne |
est le nombre de tirages de probabilité maximale, c'est la
valeur moyenne.
