Permutations, arrangements, combinaisons
Le calcul des combinaisons est très utile à celui
des probabilités. Particulièrement lorsqu'il s'agit
de compter le nombre total de cas susceptible de se présenter
lors d'un tirage simple ou combiné.
Arrangements
Voici une importante formule du calcul combinatoire.
On dispose de N objets. On tire successivement n fois un objet
au hasard parmi ces N. Quel est le nombre de combinaisons possibles?
Nombre de possibilités pour trois tirages successifs:
| Premier tirage |
fois |
Deuxième tirage |
fois |
Troisième tirage |
Nombre total |
| N possibilités |
N possibilités |
N possibilités |
N x N x N =N3 |
et pour n tirages successifs
| 1er tirage |
fois |
2ème tirage |
fois |
etc |
fois |
nème tirage |
Total |
| N poss. |
N poss. |
... |
N poss. |
Nn |
Les mathématiciens appellent cela des arrangements
de N objets n à n
mais ils s'empressent de préciser: arrangements avec
répétition, car après chaque tirage
on remet dans le paquet l'objet tiré.
Arrangements sans répétition
Si l'on ne remet pas l'objet tiré dans le paquet, le choix
d'objets diminue d'une unité à chaque tirage, et la
formule devient
dans le cas de 3 tirages (n = 3): N fois (N-1) fois (N-2)
dans le cas de n tirages: N fois (N-1) fois (N-2) fois ... fois
(N-(n-1)), aussi égal à
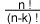
| |
le symbole "!"
est celui de la factorielle, ou produit des nombres entiers
de 1 à n |
C'est la formule des arrangements sans répétition,
dont le symbole est Ank.
Le cas particulier des permutations
Lorsque l'on effectue autant de tirages sans répétition
qu'il y a d'objets à tirer, on a le cas particulier où
n = N : au dernier tirage, on n'a plus qu'un objet,
et la formule ci-dessus devient
N.(N-1).(N-2). ... . (N-N+1) = N.(N-1).(N-2). ... .1 = N
! (factorielle de N)
On appelle cela les permutations de N objets:
c'est le nombre d'ordres différents dans lesquels on peut
placer N objets. Illustrons cela par le dénombrement de toutes
les manières dont on peut ranger les lettres B, C et D:

Voici aussi toutes les permutations de la suite de lettres A, B,
C et D:
 |
On voit que A est
en première position dans 6 cas (en rouge)
en seconde position dans 6 cas (en bleu)
en troisième position dans 6 cas (en vert) et
en quatrième position dans 6 cas (en jaune) |
| La formule ci-dessus donne bien (pour N = 4):
4 ! = 4 x 3 x 2 x 1 = 24 permutations |
Combinaisons
Tant les arrangements que les permutations tiennent compte de l'ordre
dans lesquels sont tirés les objets: "ABCD" est
considéré comme différent de "BADC".
Ce n'est pas le cas pour les combinaisons.
Combinaisons sans répétition
On peut comprendrer que le nombre de combinaisons sans répétition
de n objets k par k, notée Cnk,
est égal au nombre correspondants d'arrangements, divisé
par le nombre de permutations de k objets:
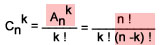
Cette formule convient pour dénombrer les
tirages sans répétition (un objet, une fois tiré,
n'est pas replacé)) sans tenir compte de l'ordre.
Combinaisons avec répétition
On peut montrer que le nombre de combinaisons
sans répétition de n obkets k par k est
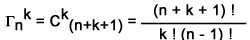
|


