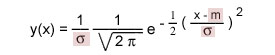La loi normale en pratique

Récapitulons

La loi normale est bien adaptée au cas où des tailles d'événements sont soumises au hasard ou à un ensemble de facteurs eux-mêmes soumis au hasard.

Elle exprime la densité de probabilité attachée à chaque mesure possible. Elle s'exprime mathématiquement par la formule

où	x est la mesure prise comme variable aléatoire
	y est la densité de probabilité de la mesure
	m est la mesure moyenne et correpond à la densité maximum
	est l'écart-type (moitié de la largeur qu'a la courbe au niveau de ses points d'inflexion)

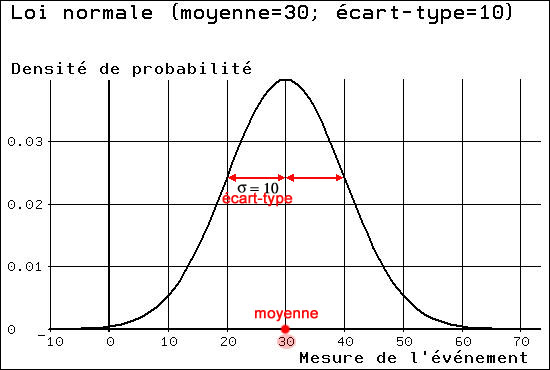
Cette formule est représentée par une "courbe en cloche", où se visualisent aisément la moyenne et l'écart-type:

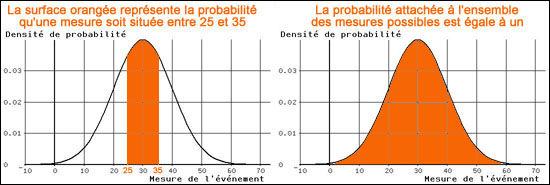
Déception !

Lorsque nous avons cessé de nous limiter aux nombres entiers, nous avons dû renoncer à attacher une probabilité à chaque nombre, pour l'attacher désormais à des intervalles de nombres. C'est pourquoi la courbe ci-dessus est une courbe des densités de probabilité, et nous avons déjà remarqué qu'elle a la nature d'une dérivée. C'est pourquoi la probabilité d'un intervalle est l'intégrale de la densité dans cet intervalle, ce qui se représente par la surface comprise sous cette courbe dans cet intervalle.

... avec pour conséquence que la surface totale, sous cette courbe, est égale à 1.

Nous nous attendons maintenant à ce qu'une formule nous permette de calculer ces probabilités pour tout intervalle souhaité. Eh bien, non! Motif: la fonction y(x), donnée plus haut, n'est pas "intégrable": elle n'a pas d'intégrale. Les mathématiciens en sont alors réduits à estimer ces valeurs par des méthodes numériques, ce qui leur permet d'établir le tableau suivant, pour le courbe normale réduite ("réduite": pour rappel: m=0 et =1).

Remarque: les valeurs de la colonne de droite sont symétriques par rapport à la valeur centrale (0,5), en sorte que la moitié d'entre elles peuvent être calculées à partir des autres.

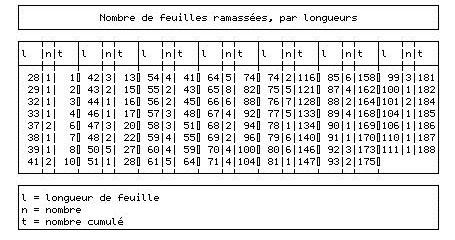
A quoi reconnaît-on une distribution "normale"?

J'ai ramassé hier au hasard 200 feuilles d'un chêne, arrachées par les premiers vents d'automne, et les ai mesurées. Seules 188 se sont avérées mesurables. Voici les mesures obtenues.

En regroupant ces mesures par intervalles de 10 mm, on peut les représenter comme suit:

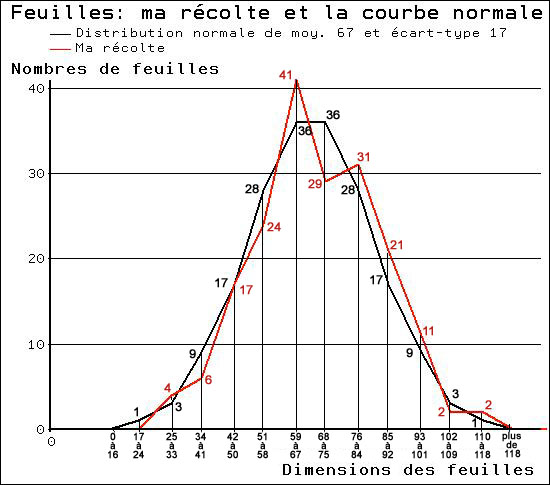
Visuellement, cette distribution ressemble à une distribution normale . En examinant les chiffres, on peut penser qu'il s'agit de celle ayant pour moyenne 67 et pour écart-type 17.

Voici la comparaison de ma récolte avec cette distribution normale.

Une autre récolte donnerait un résultat différent, et conduirait sans doute à une courbe normale légèrement différente.

On reconnaît qu'une distribution observée est "normale" au fait qu'elle correspond au tableau des probabilités donné plus haut