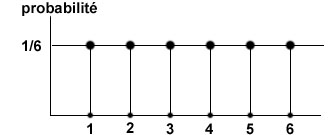
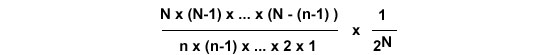Lois de probabilités

Le hasard, l'aléatoire

Le hasard n'est jamais absolu. Si je dis "je marche au hasard", mon itinéraire se limitera aux lieux accessibles à pied: je ne me retrouverai pas au Mexique. Si je lance un dé, je n'obtiendrai pas d'autres chiffres que 1,2,3,4,5 ou 6. Si je mesure la taille d'un soldat pris au hasard, je sais que cette mesure restera dans certaines limites.

Au-delà de cette question de limites, le hasard est aussi encadré par des lois: certains événements sont plus probables que d'autres. Avant même de procéder au hasard, on a une certaine idée des "chances" (de la probabilité) d'obtenir chacun des résultats possibles.

Ces chances s'expriment par des "lois de probabilités".

La probabilité constante, uniforme

Par exemple, si je lance un dé, il a une chance sur six de s'arrêter à chacun des chiffres 1 à 6, ce qui peut se décrire par une courbe (ici une droite) de probabilité

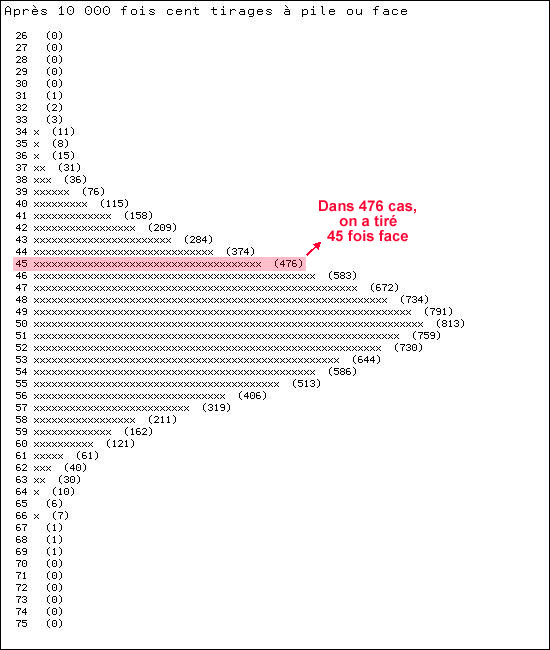
ou par une formule:

p_n = 1/6 (la probabilité d'obtenir tout nombre entier n entre 1 et 6 est égale à 1/6)

Lorsque le hasard est vraiment seul en cause, nous avons vu qu'on cherche à se ramener à des cas de probabilité uniforme, comme dans le tirage d'une carte, d'une bille dans un sac, d'une combinaison de quatre lettres, etc.

Loi de probabilité "normale"

La probabilité est une chose. Les tirages réels en sont une autre. Ainsi, à pile ou face on a une chance sur deux d'obtenir "face", mais si on lance cent fois la pièce, on n'obtiendra pas toujours 50 piles et 50 faces!

D'où, un nouveau problème de probabilité: si je lance cent fois la pièce, combien ai-je de chances d'obtenir 50 faces? Et d'en obtenir 49, 48, ...?

Commençons par une expérience: je confie à mon ordinateur le soin d'effectuer 10 000 fois ces cent lancers, et voici ce que j'obtiens

Pouvait-on s'attendre à un tel résultat? En partie, oui:

Par contre, on peut être surpris par la forme évasée des extrémités de la courbe.

Question importante: ne pourrait-on pas calculer la probabilité de chacun de ces résultats?
Réponse: oui, c'est possible. Il suffit d'appliquer habilement la méthode et les formules exposées par ailleurs.

Le résultat: la probabilité d'obtenir n faces lors de N tirages est

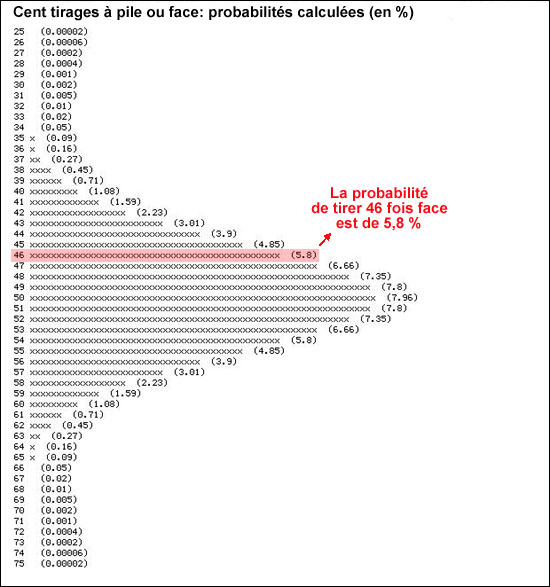
Pour N = 100, cela donne le graphique suivant pour les valeurs de N comprises entre 26 et 75 (pour les autres valeurs, les probabilités sont très très petites: par exemple, la probabilité d'obtenir 100 faces est de 7,89 x 10^-29 !